Inverse Determination of Freezing Protocols for Transplant Organs
![]()
A fully automatic procedure for maximizing the freezing rate in an organ while maintaining the local thermal stresses below a specified level throughout the arbitrarily shaped and sized three-dimensional organ made of different materials was developed. This was achieved by determining correct variation of unsteady temperature distribution on the walls of the three-dimensional freezing container. My time-accurate finite element computer program was used to predict unsteady heat conduction with phase change and thermal stresses within the realistically shaped organs. My parallel genetic algorithm optimization program (PGA) was then used to achieve nonlinear constrained optimization of time-varying container wall temperature distribution so that the prescribed maximum allowable thermal stress levels are never exceeded throughout the organ.
The surface variation of temperature on the spherical container wall was
approximated with biquadratic Lagrange polynomials using 9 control points for
each of the large six deformed quadrilateral patches forming the container wall
thus resulting in a total of 26 design variables.
The transient temperature distribution and stresses were computed at every
point of the organ. From this, the actual local cooling rates and thermal
stresses were determined at each point of the organ. The genetic
algorithm was used after certain time interval to optimize the temperature at
each of the control points on the spherical container surface. That is,
the new temperature distribution on the container walls was determined so that
it maximizes the average cooling rate in the organ for the given time interval
while keeping the local thermal stresses in the organ below a user specified
maximum allowable value. The algorithm is outlined below.
|
|
The objective function, also referred to as fitness, F, that was maximized every time interval was
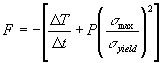
where ![]() and
and ![]() and P is a user specified penalty
term.
and P is a user specified penalty
term.
The three-dimensional freezing protocol simulation and optimization
algorithm was applied to geometry composed of three domains. The outer
domain was a spherical freezing container. Within the spherical container
was a kidney consisting of a medulla and the imbedded cortex as shown below.
|
|
A tetrahedral grid was used to discretize the volume of all three domains. The time interval, Dt, between each application of the optimizer was set to 5 minutes. The penalty term in the objective function, P, was fixed at P = 100 when the maximum Von Mises stress in the kidney domain, smax, was greater than the local yield stress, syield. The penalty term was P = 0 for all other situations.
The genetic algorithm (GA) used 4 bit strings to represent each of the 26 design variables (container surface node temperatures). Each of these variables was allowed to vary from 20oC to –30oC. A uniform crossover operator was used with a 50% chance of crossover. A fixed population size of 31 was used with a 2% chance of mutation. Each optimization cycle was run for 20 generations. Each optimization cycle was executed on our distributed memory parallel computer composed of commodity computer components. Each analysis run, which was composed of simulation of three-dimensional heat conduction with a moving freezing front in this multi-domain region including thermal stress analysis, required 3.5 minutes on a single CPU. Parabolic elements were used for heat conduction analysis and linear elements were used for the stress analysis. The heat conduction grid was composed 8245 nodes and 5184 tetrahedral elements and the stress analysis grid was composed of 1315 nodes and 5184 tetrahedral elements. A time step of 15 seconds was used for each transient heat conduction analysis.
The animations below show the freezing process as it progresses through time. It can be seen that by 50 minutes, the kidney has been completely frozen without violating the yield stress.
|
Animation of temperature contours along slice at y=0 for every 5 minute interval |
Animation of temperature contours along slice at z=0 for every 5 minute interval |
In this proof of concept simulation it has been demonstrated that it is possible to control the damage caused by the thermal stresses during freezing of organs by periodically optimizing the freezing container surface temperature distribution. However, more accurate thermophysical data, finer spatial and temporal discretization, more diverse tissue subdomains, more complicated geometries of organs and containers, and more accurate physical modeling of the freezing process are required before this concept can become a reality.
![]()

