In this project I consider the problem of multidisciplinary design and optimization (MDO) of a diffuser for a steady, incompressible magnetohydrodynamic flow. Given a fixed diffuser shape, the optimizer should find the distribution of the wall magnets that will maximize the static pressure increase from inlet to outlet. This design problem is solved through the use of my genetic algorithm based optimization program coupled with my finite element based MHD simulation program. The optimization was performed on our parallel computer composed of commodity PC components.
The Reynolds number is 486, based on the diffuser outlet height. For this Reynolds number there are two large separation regions that result in a large loss in the diffuser's efficiency.
The magnetic field distribution along the diffuser bottom wall was parameterized with two B-splines, one spline for the normal component and one spline for the tangential component. The control points were encoded with 9-bit binary strings and were allowed to move vertically from -1.0 to 1.0 and horizontally along the full length of the diffuser except the end control points that were fixed. A 10-bit string was used to encode the magnetic field strength that was allowed to vary from 0 to 1.2 Telsa. Altogether, a total of 20 design variables were used.
Two optimization runs were made simultaneously, each starting from different random populations and each using 16 processors. Each used micro GA, a population size of 15, uniform crossover, a 50% probability of crossover, tournament selection, and no mutation. In about 30 hours, both optimization runs completed 100 generations.
By generation 100, run 1 achieved a pressure increase of .207 Pa and
run 2 achieved a pressure increase of .228 Pa. For comparison,
the diffuser without an applied magnetic field achieved a pressure increase
of .05 Pa. Figure below show the streamlines for the diffuser with
the optimized applied magnetic field. For comparison, the figure below
shows the streamlines for the diffuser with no applied magnetic field.
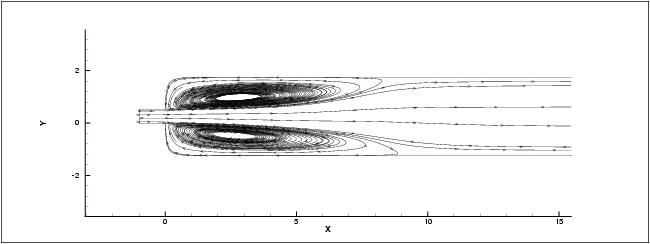
Streamlines with no applied magnetic field |
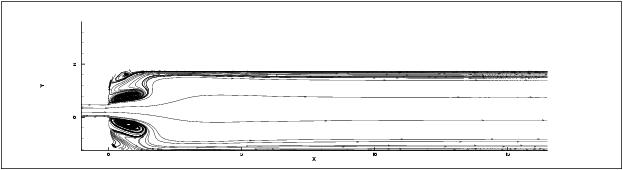
Streamlines with optimized applied magnetic field |
It is not difficult to design by hand magnetic fields that will
completely suppress the vortices. Streamlines for such a configuration
is shown below. One would think that this would result in a large pressure
increase but, in fact, the pressure drops dramatically. The distributed
magnetic field that will suppress the vortices is so strong (approximately
2.0 Tesla in this case) that it exerts a braking effect on the fluid similar
to what occurs in Poisuille-Hartmann flow. The pressure drop due
to the magnetic braking far outweighs the pressure increase due to the
suppression of the vortices. This demonstrates why optimization is critical
for finding improvements in design situations that include complex interactions
among multiple physics.
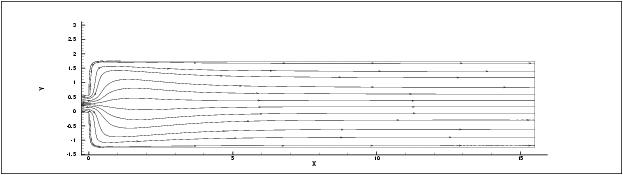
Streamlines for applied magnetic field that suppresses vortices |